Machine learning is a field that is inextricably intertwined with the field of optimization. Countless machine learning techniques depend on the optimization of a given objective function; for instance, classifiers such as logistic regression, metric learning methods like NCA, manifold learning algorithms like MVU, and the extremely popular field of deep learning. Thanks to the attention focused on these problems, it is increasingly important in the field to have fast, practical optimizers.

Therefore, the need is real to provide a robust, flexible framework in which new optimizers can be easily developed. Similarly, the need is also real for a flexible framework that allows new objective functions to be easily implemented and optimized with a variety of possible optimizers. However, the current landscape of optimization frameworks for machine learning is not particularly comprehensive. A variety of tools such as Caffe, TensorFlow, and Keras have optimization frameworks, but they are limited to SGD-type optimizers and are only able to optimize deep neural networks or related structures. Thus expressing arbitrary machine learning objective functions can be difficult or in some cases not possible. Other libraries, like scikit-learn, do have optimizers, but generally not in a coherent framework and often the implementations may be specific to an individual machine learning algorithm. At a higher level, many programming languages may have generic optimizers, like SciPy and MATLAB, but typically these optimizers are not suitable for large-scale machine learning tasks where, e.g., calculating the full gradient of all of the data may not be feasible. informations.

Given this situation, we have developed ensmallen a flexible optimization framework. Which makes it easy to combine nearly any type of optimizer with nearly any type of objective function, and has allowed us to minimize the effort necessary to both implement new optimizers and to implement new machine learning algorithms that depend on optimization.

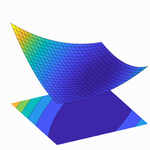
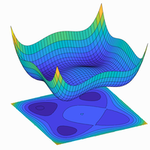
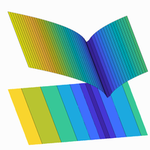
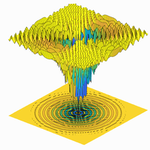
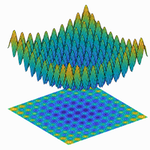
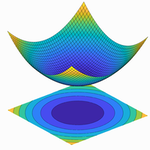
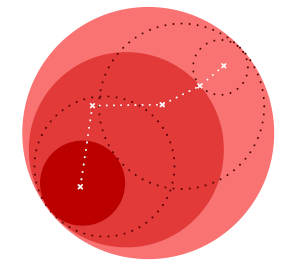
This visualization allows us to see how many popular optimizers perform on different optimization problems. Select a problem to optimize, then select an optimizer and tune its parameters, and see the steps that the optimizer takes plotted in red. Note you can compare how different optimizers perform on a given problem in the second graph. As you try a given problem with more optimizers, the objective function vs. the number of iterations is plotted for each optimizer.

In order to facilitate consistent implementations, we have defined a FunctionType API that describes all the methods that an objective function may implement. ensmallen offers a few variations of this API to cover different function characteristics. This leads to several different APIs for different function types: how to implement the different types of functions f(x) that ensmallen can handle

Each of these types of objective functions require slightly different methods to be implemented. In some cases, methods will be automatically deduced by the optimizers using template metaprogramming and this allows the user to not need to implement every method for a given type of objective function.